函数式设计导读系列（二）

发表于 更新于 分类于

有限与无限的游戏

美国哲学家詹姆斯·卡斯写过一本书《有限与无限的游戏》，向我们展示了世界上至少有两种类型的“游戏”。有限的游戏，具有明确的开始和结束，其目的在于赢得胜利；无限的游戏，没有固定的开始和结束，旨在让游戏永远进行下去。有限的游戏在边界内玩，无限的游戏玩的就是边界。

Bob 大叔在解释函数式的惰性时，翻出了那款经典的保龄球游戏。今时不同往日，他玩起了无限的游戏。

我们先把保龄球的游戏规则过目一遍，头脑中有个怎么玩的印象就好。

保龄球每个玩家每局有 10 个计分格(frame)。每个计分格玩家最多有 2 次投球(roll)机会，但第 10 个计分格最多有 3 次投球机会。每个计分格的得分，是击倒的球瓶总数，再加上全中(strike)或补中(spare)的奖励分。全中，指第一球就击倒了所有 10 个球瓶；得分为 10 分，再加上接下来的 2 次投球（属于下一个或之后的计分格）所击倒的球瓶数。补中，指在一个计分格中，用两次投球才击倒所有 10 个球瓶；得分为 10 分，再加上接下来的 1次投球（属于下一个计分格）所击倒的球瓶数。第 10 个计分格有点不同。如果在第 10 个计分格投出全中或补中，则能获得额外的投球机会来完成这个计分格；如果是全中，能获得 2 次额外投球；如果是补中，则能获得 1 次额外投球。这些额外的投球，只用于计算第 10 个计分格的得分。

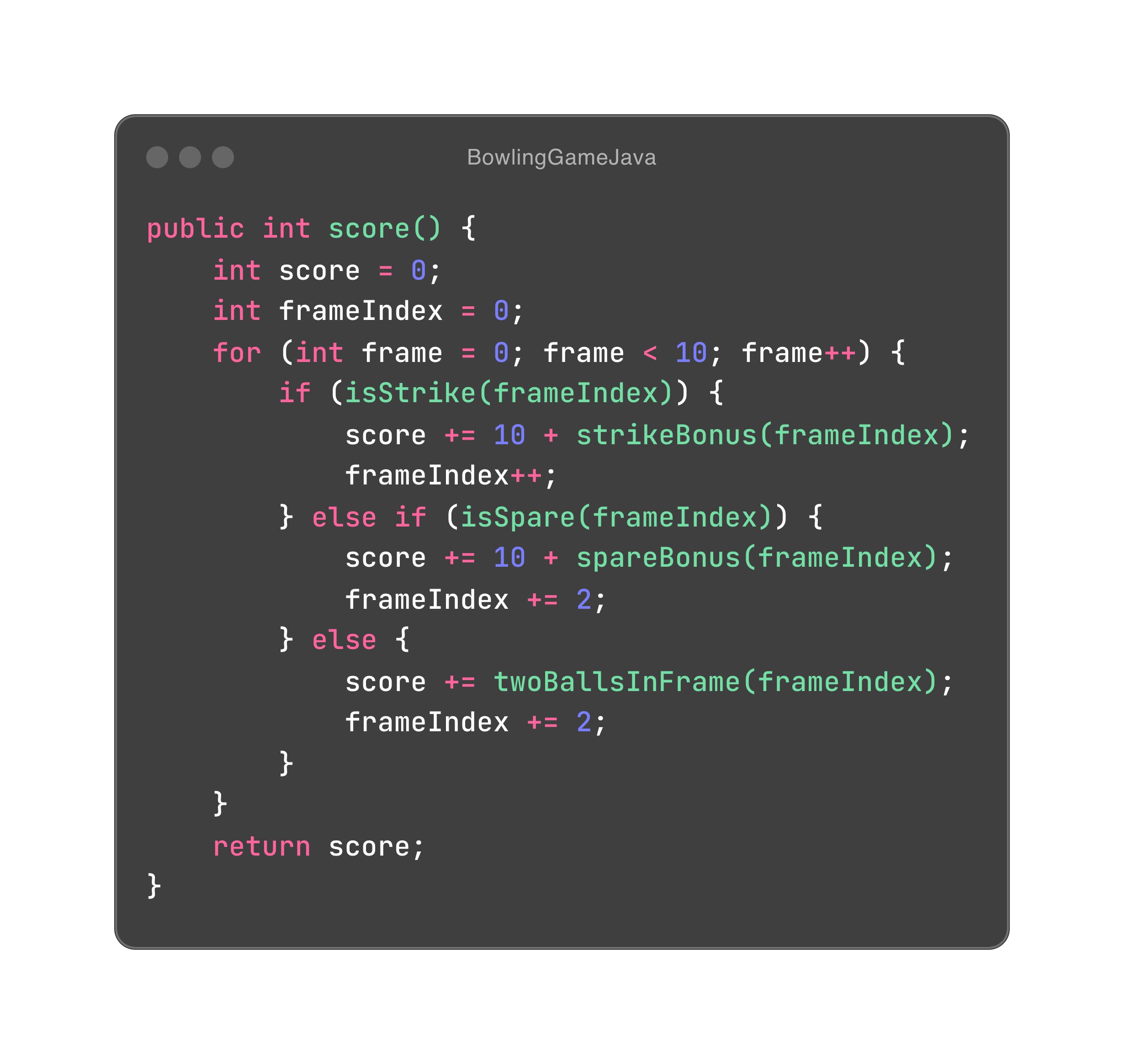
BowlingGameJava.png

在上面 Java 版本的代码中，几乎是无意识地，我们把得分计算 score +=和投球的次序 frameIndex++揉到了一处。这是自然思考的结果，因为累积 frameIndex 就重现了投球的时序，得分跟着时序在规则（isStrike, isSpare?）的安排下一步步累加。但是事实上，因为不得不识别出影响每个计分格的所有投球，真正时序耦合的是 frameIndex 和当前计分格的得分计算，而不是总得分。所以，这段代码可以重构下，将总得分的计算放到了最后。

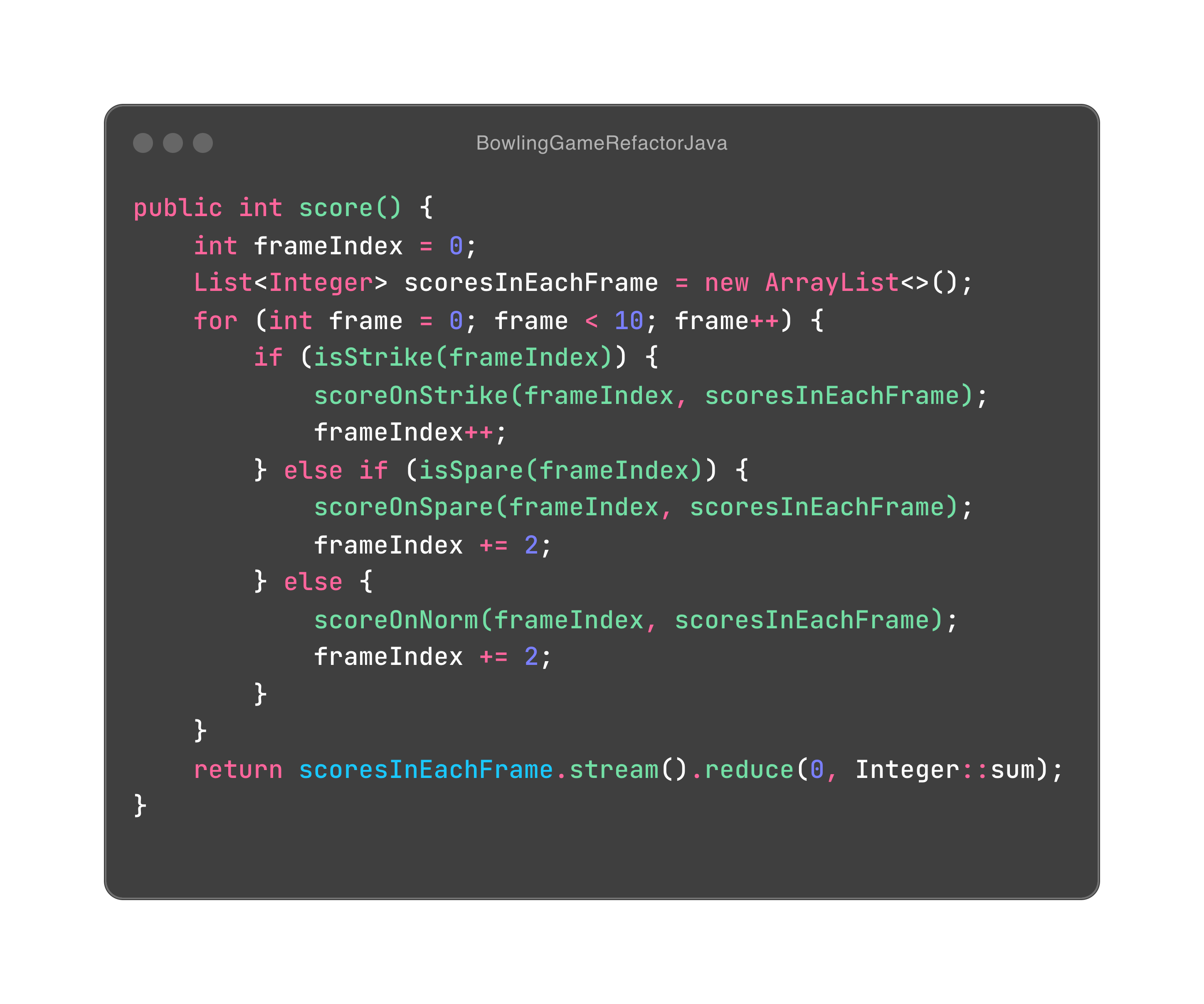
BowlingGameRefactorJava.png

重构方式很简单，新增一个 scoresInEachFrame 列表，把每一个计分格的得分加进去，最后做求和。

这样的代码几乎可以很容易地写成像下面一样 Clojure 的 loop...recur 形式。

BowlingGameRefactorClj.png

转换成这种形式之后，我们至少能知道两件事情。第一，frameIndex 这类索引让代码显得很难读；第二，frame 这是个控制量，它不参与实际的计分运算。

对于第一种坏味道，我们可以用列表的解构来解决。这里面凸显一种思想，新的列表是从旧的列表演变出来的，正如 map 函数所做的那样。

BowlingGameFramesClj.png{:height 437, :width 476}

代码中 (loop [remaining-rolls frames]...)正是这种思想的延续，在每次递归调用中，remaining-rolls 减少了，而 frames 增加了，它们之间的演化（映射）逻辑就是游戏的计分规则（Strike等）。当然，这段代码和上面的代码并不等价，原因是它没有提前计算每个计分格的得分，而是保留下所有计分格，例如在 Stirke 情况下，frame 是 [10 X Y] 这种形状。

对于第二个问题，既然不参与计分格的计算，最好是忘得越远越好。也就是说，假如我们想永远玩下去，那么这种程序最好也能正确计算出得分，直到我们想终止为止。

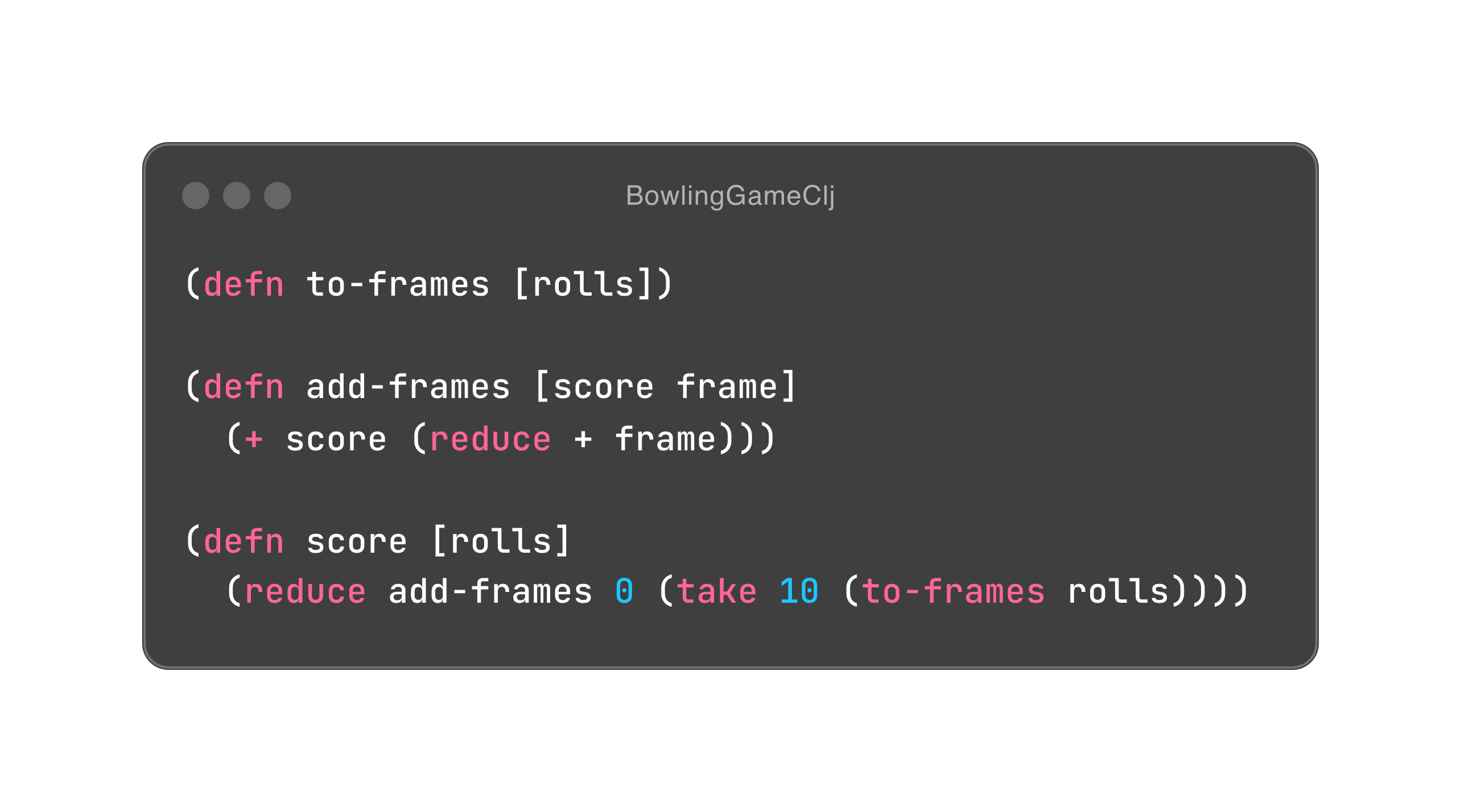
BowlingGameClj.png

在无限游戏的场景下，rolls 可以无限投掷，我们就可以无限地推迟从计分格中获得总分的决定。遗憾的是，保龄球游戏中有一条定胜负的终止规则，每局只有 10 个计分格，所以它不是无限游戏。在程序计算总分的最后，取出了 10 个计分格。

惰性，无限可能！

Bob 大叔分析说惰性之所以需要，是因为这样做可以把需要做的事情和需要做的量分离开来。延迟需要多少量这个决定到最终用户的手上。

惰性是实现无限游戏的手段，而无限是帮我们扫清聚焦计算（厌恶那些 indexes 吧）障碍的思维方式。试想，列表元素都无限多了，你还会思考越界吗？你只会想我该怎么这个游戏一直玩下去。

惰性列表时一个知道如何计算下一个值的对象。惰性列表是伪装成列表的迭代器。