函数式设计导读系列(一)
我是 Bob 大叔的《架构整洁之道》中文版的技术审校,也是他的扛鼎之作《敏捷软件开发:原则、模式和实践》重制版的译者。当然,再次有幸参与了大叔的新作《函数式设计》的技术审校,我想谈谈过程中个人的所学所想。
函数式设计导读系列(一) 本质说,追求不变性。
函数式设计导读系列(二) 惰性,把数量多少放到一边。
函数式设计导读系列(三) 状态,把可变性放到一边。
浓眉大眼的 OO 叛变革命?
Bob 大叔成名已久,是面向对象编程领域当之无愧的领军人物。如今,他出一本函数式编程的书籍,我想他的多数读者应该会感到疑惑:没想到你浓眉大眼的,居然也叛变了“革命”。Bob 大叔叛变了吗?他的这本书和他之前的诸多作品文脉想通,有继承也有创新,落脚点还是实用。我用电梯演讲的方式概括了这本书的内容和优势。 对于:Bob 大叔的读者多数是面向对象编程的熟练手
一问三连,一发入魂
决定读不读一本书,最好的方式是带着疑问去检索答案。我拿到这本书,脑子中闪现的一个问题就是函数式设计是作为面向对象设计的对立面提出来的吗?当我翻开前面几页,发现 Bob 大叔居然用了 Clojure 这门 Lisp 的方言来阐述观点,不由得心头一紧,这门编程语言受众很窄,恐怕会劝退很多读者呀!写过如此之多畅销书的 Bob 大叔不会没有意识到这点,那他的目的何在?我把书从头粗粗地翻到末尾,闭目凝神,回想 2010 至 2020 年这十年间函数式编程语言红极一时又式微的过程,叠加 genAI Copilot 辅助编程的滔天巨浪,不免心有戚戚,喟然叹曰:现在再来讨论编程范式,有用吗?
FD 是作为 OOD 对立面提出来的吗?
Bob 大叔为什么要用 Clojure 语言,这种小众语言我又用不上,学了等于白学?
如果我工作中没有用到函数式编程语言,这本书是不是对我帮助就不大了?
真相只有一个!
你觉得函数式编程的本质是什么?一切皆函数(注:纯函数)。这个回答怕是贴着面向对象编程的脸喊出来的。Bob 大叔在书中就不这么说的,他的厉害之处就在于:别整这些玄乎饶舌的概念,给我上代码,拉出来溜溜,拿捏几下,我就知道你姓甚名谁,写下来,完了还给自己的前一本书压个韵。
Bob 大叔在《架构整洁之道》中提出了编程范式的真相 —— 约束程序的执行,告诉我们不能做什么。
为什么要对程序的赋值操作做限制呢?原因在于赋值带来程序的时序耦合,显然时序耦合是让程序复杂(难懂)的诱因之一。我们看看一段计算前十个整数的平方和的 Java 程序,这段程序中包含了两个变量并且都有赋值。仔细看这三段注释的 log 函数,其中第二个记录的 sum 和 i 并不是这轮循环的最终状态(sum累加之后,i 必须自增)。具体来说,调用 sumFirstTenSquareHelper(0, 1),正确的 [sum, i] 状态对是 [0, 1], [1, 2], [5, 3] … [385, 11],但是第二处记录却是错误的状态对,如 [1, 1]。也就是说,赋值的操作给了时间顺序这个坏蛋以可乘之机,让本应是原子化的变量状态出现不一致。假设放到更加混乱的多线程环境中,这段程序时不时会出现错误,这也被称为竞态条件。竞态条件是指多个线程在访问共享资源时,其执行顺序可能导致结果的不确定性或错误。
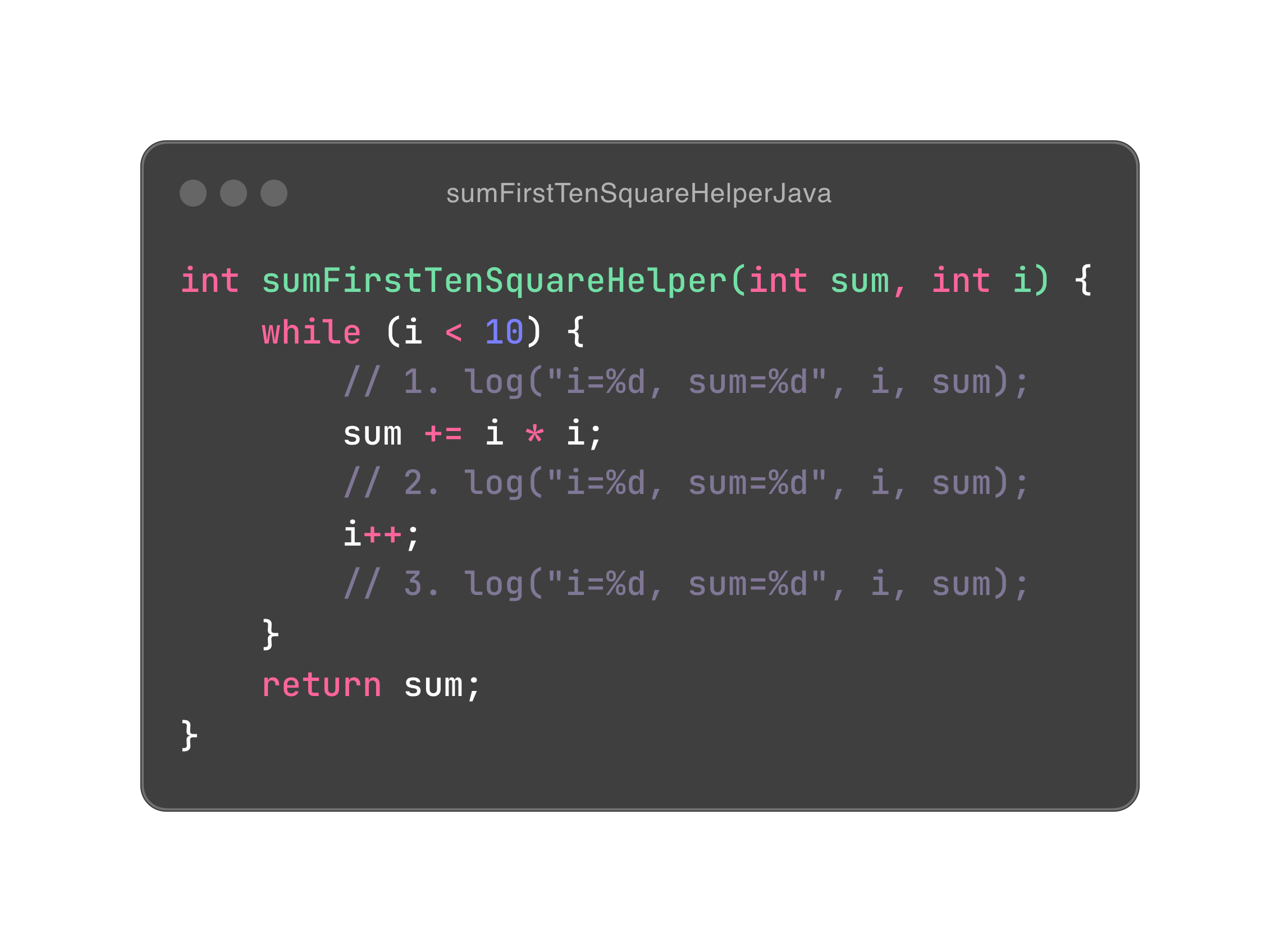
既然赋值或称对变量的改变是时序耦合的罪魁祸首,那么明智的做法自然是干掉它。我们解析下赋值的目标是什么?没错,状态的变化。完成状态的变化,通常有两种做法。第一种简单粗暴,用新的直接干掉旧的,让旧的消失于无形,俗称破坏性创新。第二种优雅得多,符合重构(refactoring)十六字心法“旧的不变,新的创建,一键切换,旧的再见”。前者是赋值,后者是替换。说白了,替换不是抹去前任痕迹,而是让旧的依然如故,以旧换新而已。
那么到底该怎么做呢?函数式编程中有两大武器,可以实现以旧换新的便宜操作。第一件是递归函数调用(recursive function call),第二件是持久性数据(persistent data)。我们知道,递归函数调用如果未到达递归出口(一般是 if 条件),那么它的栈桢就会不断累积下去,每一层栈桢都可以看作是一次以旧换新;而持久性数据是一种支持多版本的数据结构,它会尽可能地共享数据结构来避免以旧换新时数据的完全拷贝,毕竟,完全拷贝听上去就很浪费。
我们看看用 Java 程序用这两大武器实现赋值消失术。利用递归,将赋值转换成算出新值,然后作为参数传递给递归函数。因为此处的参数仅是原生类型,对于复合类型,持久性数据的威力才会发挥出来。
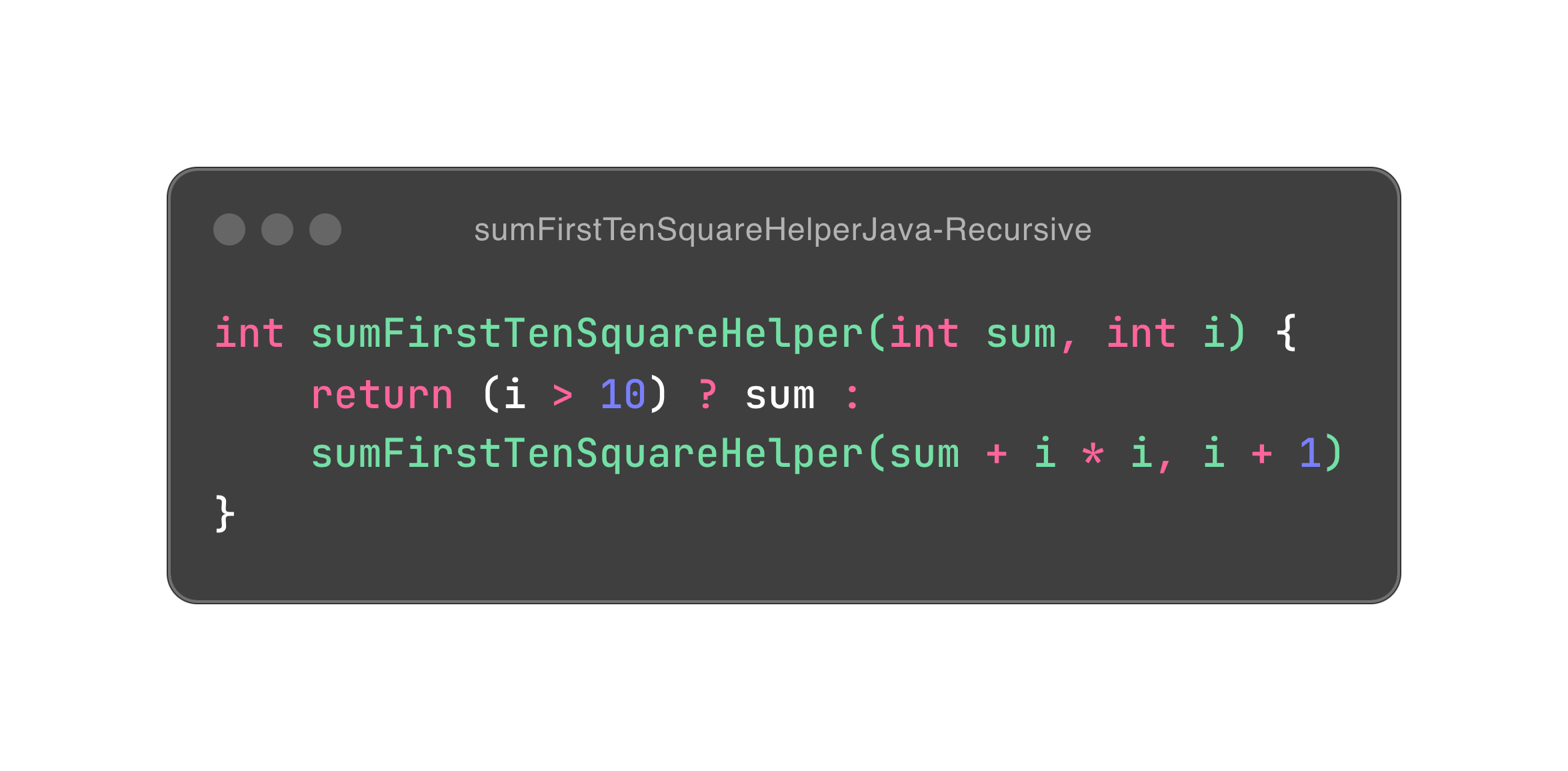
如此看来,我们已经完成了赋值的历史终结任务,但令人不安的是天边似乎还有一朵乌云——递归的代价。我们用 Clojure 同样实现一遍上面的简短程序。然后用 cider-toggle-trace-ns(如果你用 Emacs + Cider 写 Clojure 的话,顺便说一句,有兴趣的人足够多,那我会分享自己的 Emacs + Cider 配置),一旦调用该函数,就会有深深的调用栈出现。递归会让函数 call 栈桢增长,导致栈溢出。
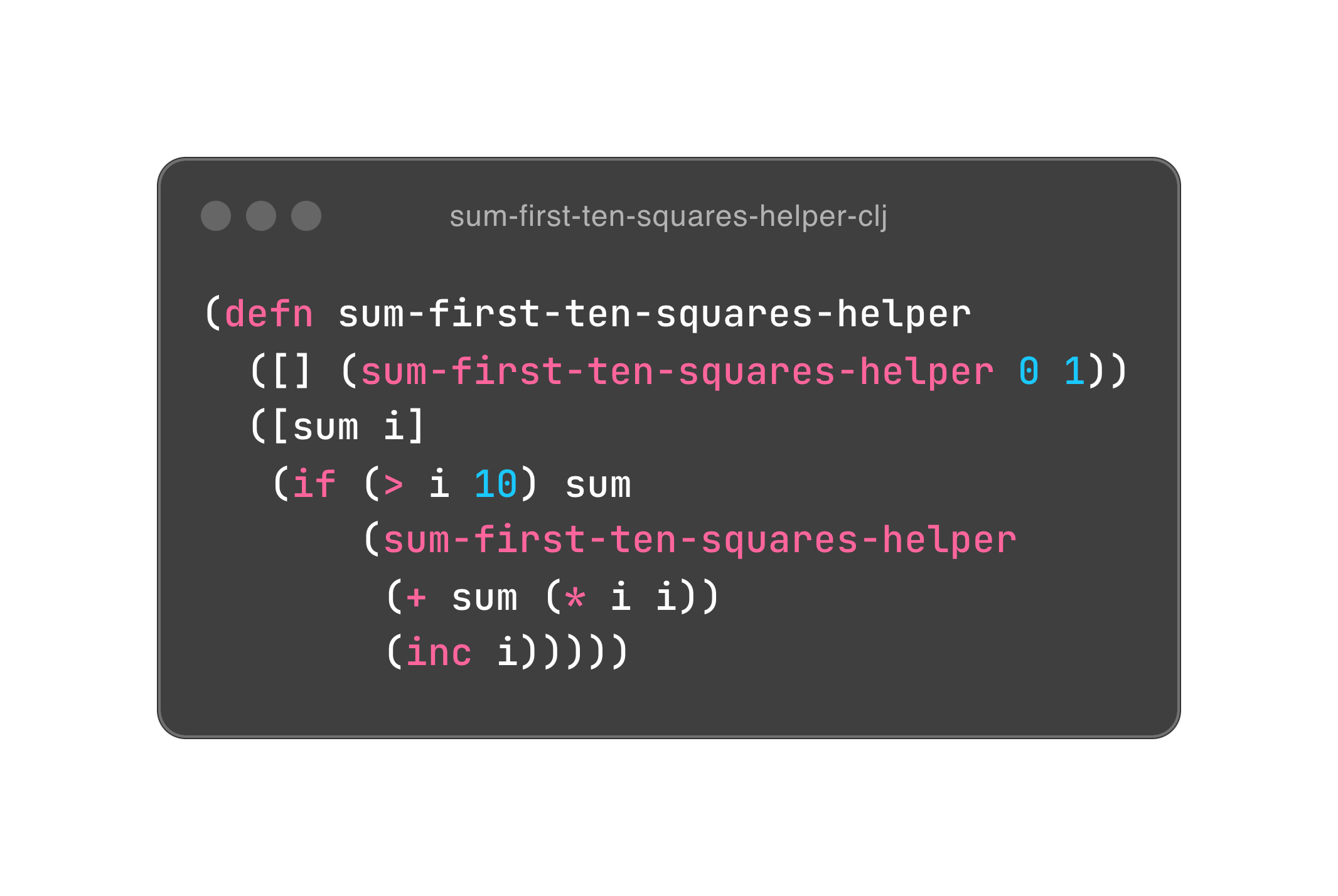

递归有代价,尾递归来优化。我们把上面的程序略作修改,把内部的函数调用名改成 recur,重新求值,再来观察一下调用栈。你会惊喜地发现,深深的栈不见了,尾递归优化(TCO)复用了栈桢,以此达到了循环的目的。所以,你会在这本书的多数程序中发现这样的结构 (loop...recur)。

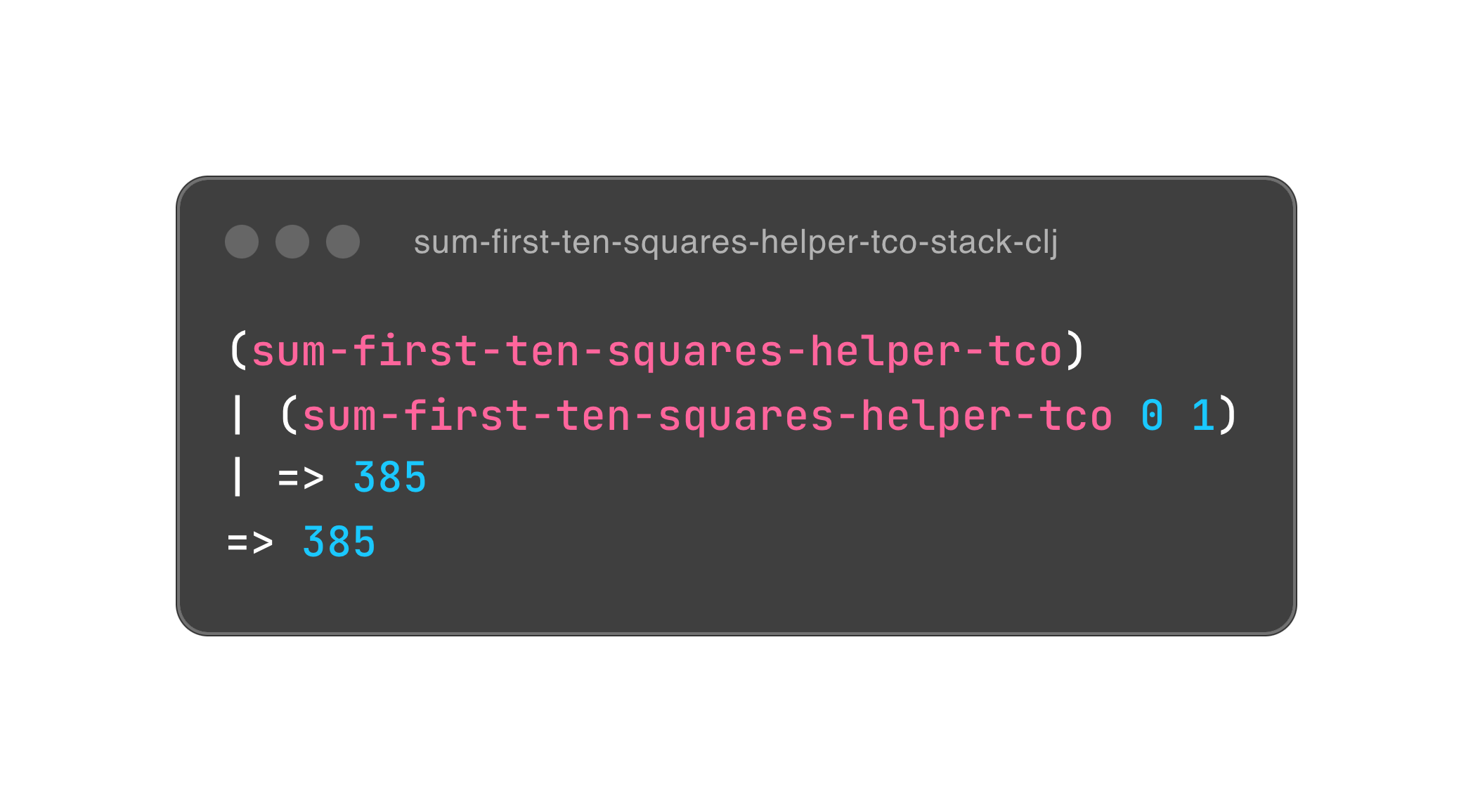
我们用两段伪代码来通观下刚刚到底发生了什么事情。对,我们用尾递归去掉了循环赋值。我们回过头来看看。 尾递归看上去很复杂,但其实很简单。上面程序展示了过程式代码改造成函数式尾递归的过程,其中最大的差异点就是消除了变量的赋值。 其实,搞了这么多新奇的手法,又是尾递归优化又是持久性数据,那都是因为计算机的开山老祖是图灵的图灵机而不是阿隆佐·邱奇的 lambda 演算,我们一直在用图灵机的实现模拟 lambda 演算。所以,总结下来就是持久性数据 (persistent data) 在递归参数中的复制以代替赋值,用 TCO 减少栈桢增长。
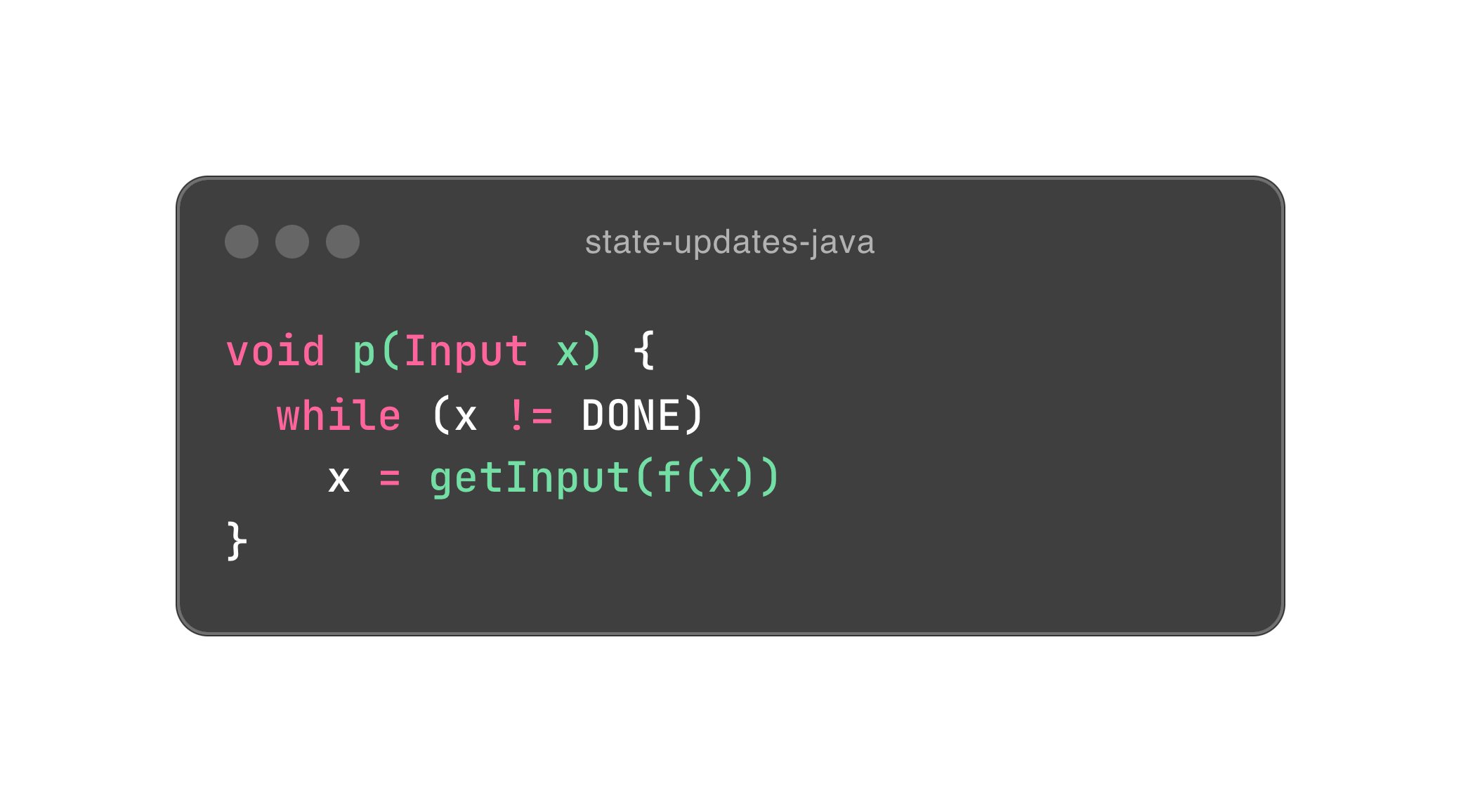
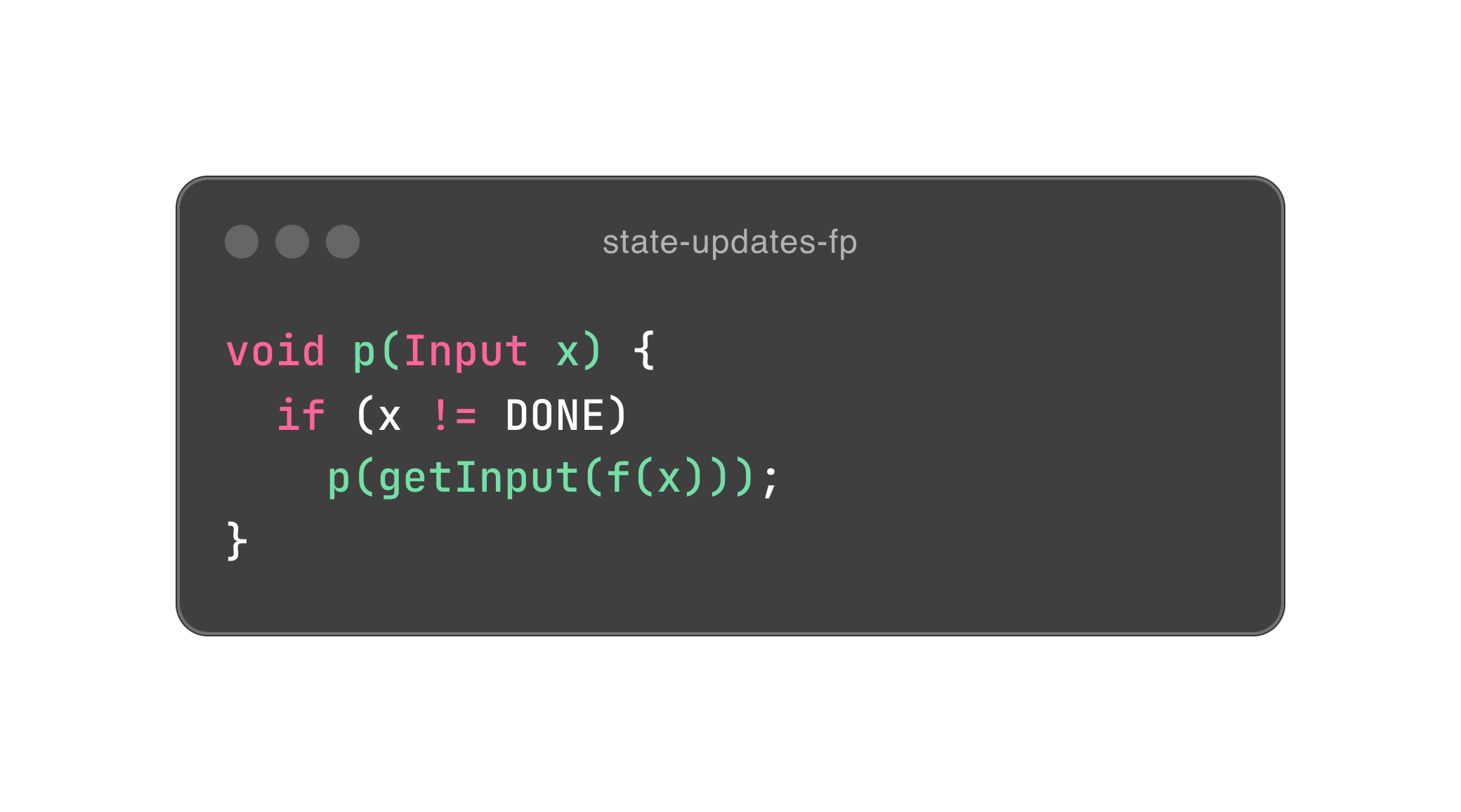
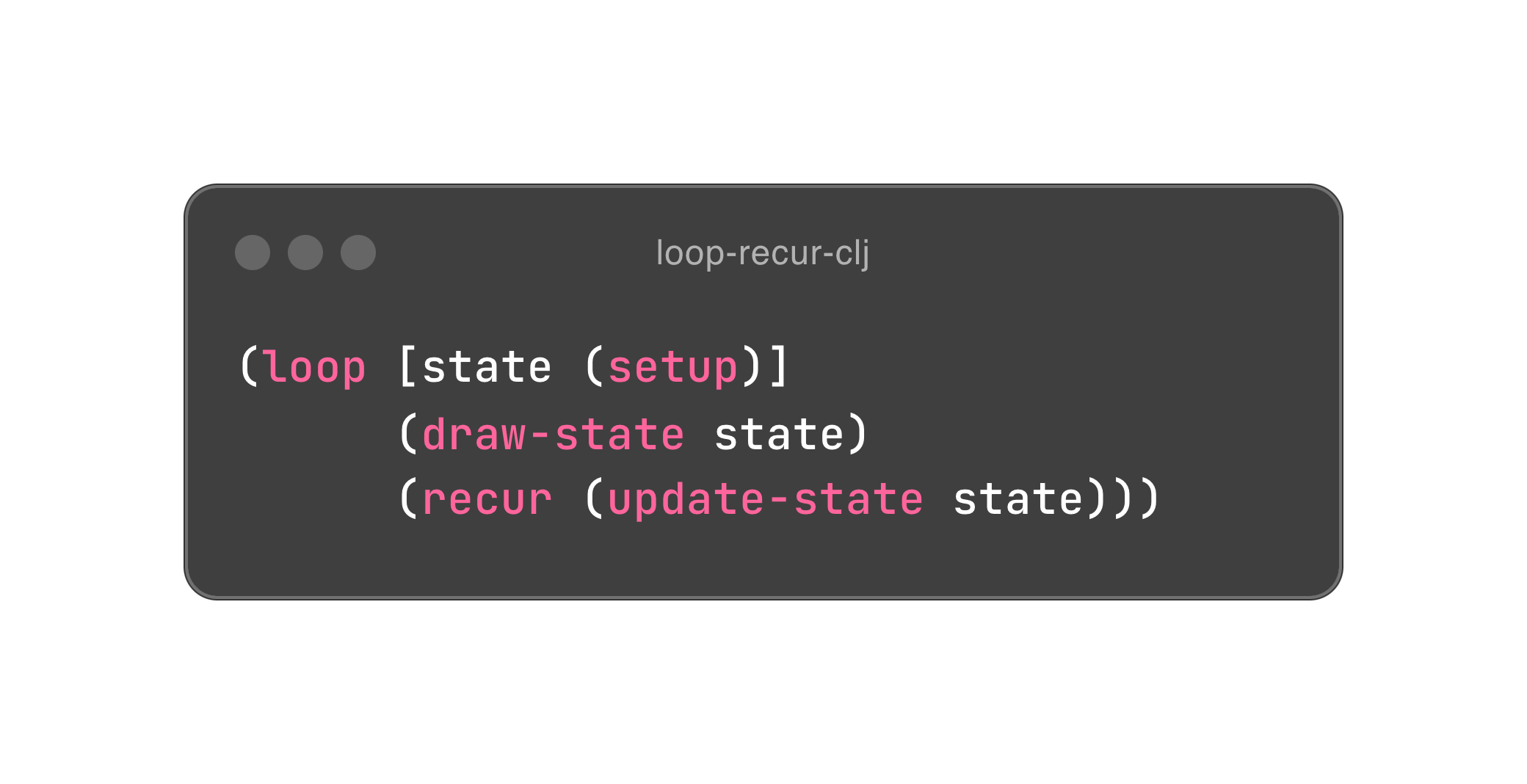
归根结底,函数式编程遵循一个朴素的原则,追求不变性。甚至可以说,函数式设计的本质就是拿捏不变性。其余的绝妙功法,我们后续再聊。